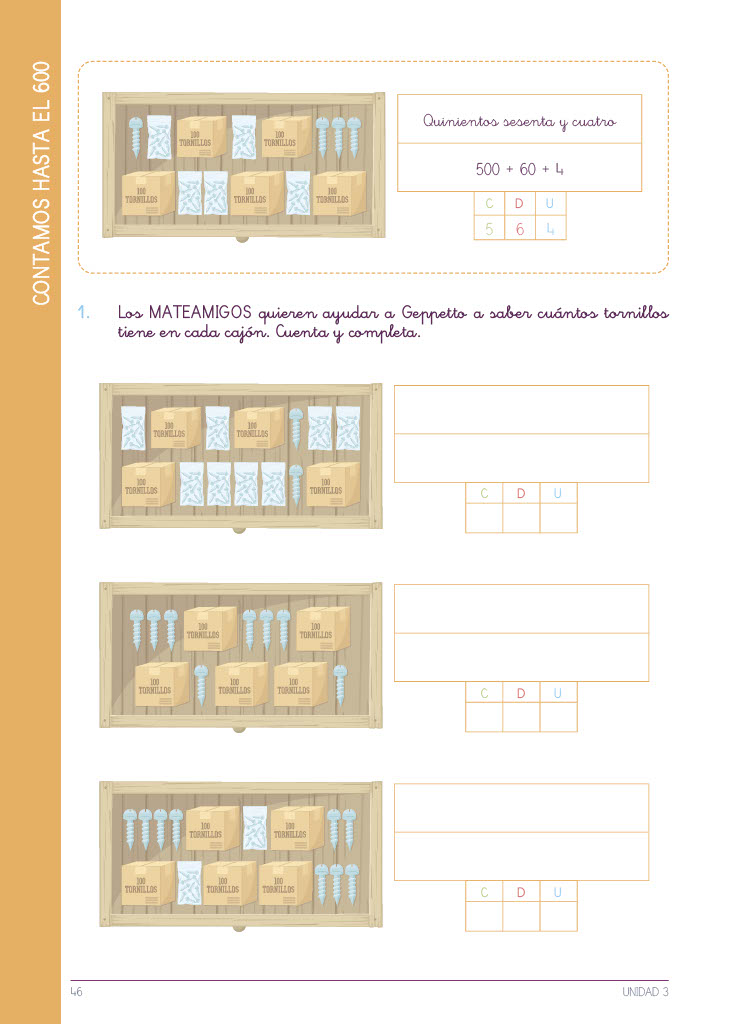
Seguimos trabajando numeración, en este caso hasta el 600. Para ello hacemos ejercicios como los anteriores ya que conocen la dinámica y les resultará más fácil.

– Formar números que vamos diciendo partiendo desde cero con material manipulable.

– Utilizar simbología de manera que puedan dibujar los símbolos necesarios para formar un número o adivinar un número partiendo de una composición dada.

– Un ejercicio completo que hacemos en clase es partiendo de un número que anotan en su pizarra tienen que:

• Escribir con letra.
• Indicar el orden de unidad que tiene cada cifra.
• Hacer descomposición aditiva.
• Representar el número con simbología.
• Representar el número con material manipulable.

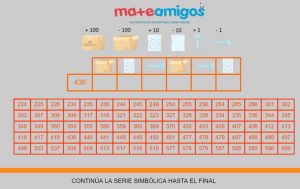
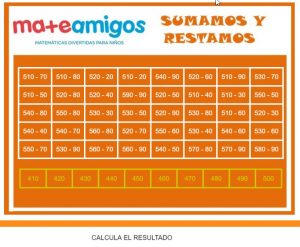
– Con las series simbólicas básicamente queremos trabajar de forma específica las fronteras de los números, es decir, el cambio de centena al sumar o restar una decena. Si estamos en el 496 y queremos sumar una decena estamos pasando del 400 al 500 al igual que si al 305 le quitamos una decena estamos pasando de 300 al 200.

– Al sumar o restar tanto centenas como unidades los alumnos no tendrán la misma dificultad que al hacerlo con las decenas. En este caso podemos utilizar la estrategia que hemos indicado varias veces en los temas anteriores. Cuando queremos sumarle una decena al 496 es más fácil que el niño piense que a 49 D le vamos a sumar 1 D para pasar a tener 50 D que junto con las unidades serían 506. De igual manera si estamos en el número 305 y queremos quitarle 1 decena es más fácil pensar que a 30 D le quito 1 D para pasar a tener 29 D que junto a las unidades serán 295.

– Para las descomposiciones incompletas  podemos ir diciendo que formen la cantidad que les va apareciendo. Partiendo de la cantidad observarán unidad a unidad lo que les falta para completar el número.

–  Otra forma es formar la cantidad que queremos conseguir e ir quitando lo que ya tenemos para que nos quede la cantidad que tenemos que anotar.

– En esta página trabajamos por primera vez la composición de números.

Si partimos de la descomposición 2 C 26 D 135 U comenzaremos por las unidades y nos daremos cuenta de que únicamente tenemos 5 y las anotaremos. Después iremos a las decenas y habrá que observar que tenemos decenas en dos casillas diferentes por lo que habrá que juntarlas para tener 9 en este caso. Por último juntaremos las centenas de cada casilla que son 1 + 2 + 2 que hacen un total de 5. Así habremos formado el número 595.

Recordamos 3 pasos que se pueden utilizar para resolver las series:

1.° Ver si la serie es ascendente o descendente.

2.° Averiguar la cantidad que va desde un número a otro.

3.° Por último hay que resolverla.

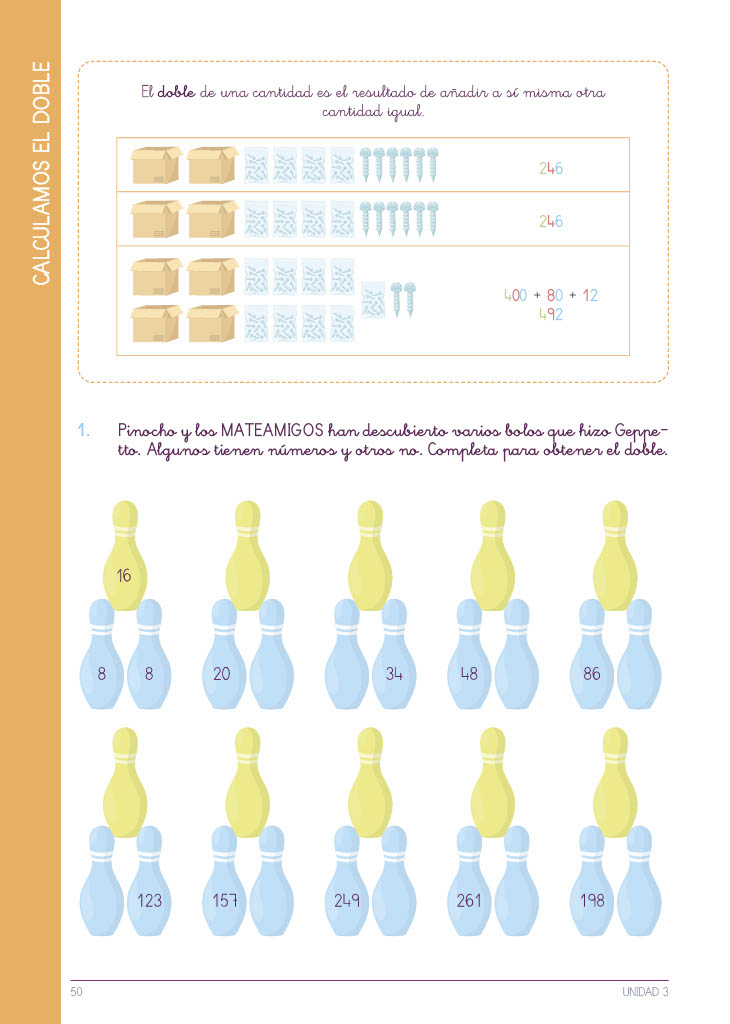
– Cuando aún no han aprendido a multiplicar, nos limitaremos a enseñarles a agregar una cantidad igual. Cuando lo dominen podemos decirles que están multiplicando por dos, como información complementaria.
– Conviene empezar por lo más sencillo, enseñar a encontrar el doble de una cantidad, con material concreto.
Podemos pedirles que tomen 5 fichas, material multibase, palillos… y luego otras 5 y digan cuántas tienen si las juntan: 10 fichas. Entonces les explicamos:10 es el doble de 5. El doble de 5 es 10 porque 5 + 5 = 10
– Cuando se practique con niños que ya empezaron a multiplicar, puede escribirse también: El doble de 5 es 10 porque 5 x 2 = 10
– Es interesante introducir ya el concepto de mitad ya que ambos conceptos están muy relacionados entre sí.
– Una vez hemos trabajado con unidades haremos el mismo trabajo con decenas completas, es decir, cogerán una cantidad de material que forme el número 40 que son 4 D y luego tendrán que coger otras 4 para formar el doble.
– Por último se hará lo mismo con las centenas.
– De esta manera se quiere conseguir que cuando quiera calcular el doble de un número de 3 cifras como pueda ser el 347, lo haga primero calculando el doble de cada una de las unidades. De esta manera calculará el doble de 300, el de 40 y el de 7 por separado para luego juntar todas las cantidades: 600 + 80 + 14 = 694

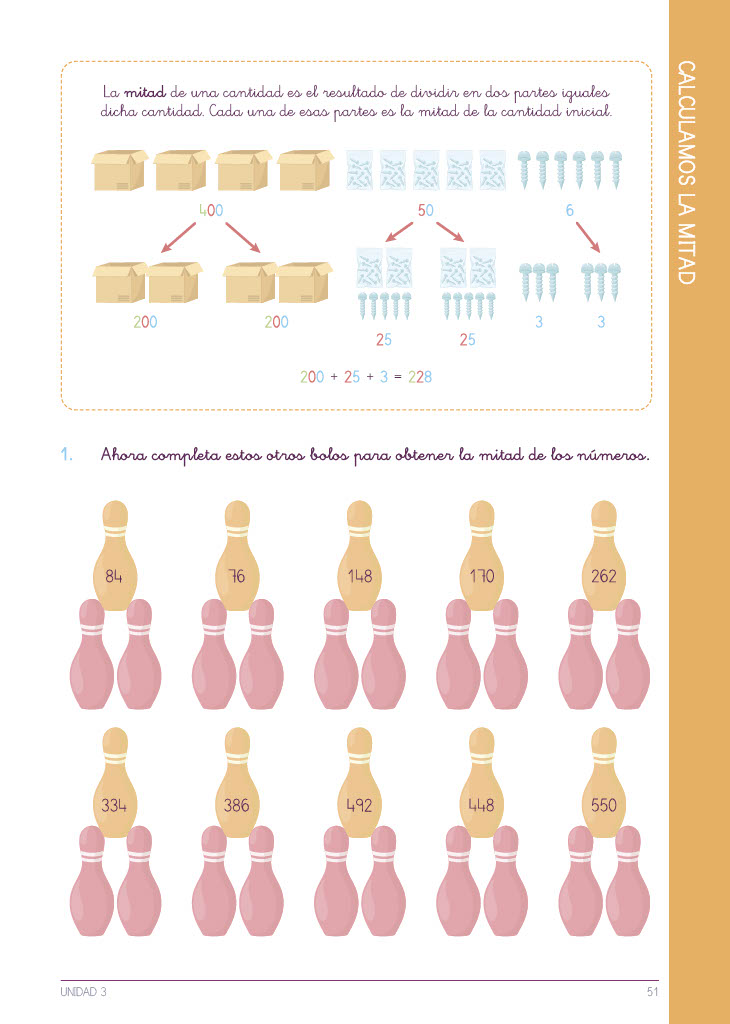
– Cuando aún no han aprendido a dividir, nos limitaremos a repartir en dos cantidades iguales. Cuando lo dominen podemos decirles que están  dividiendo por dos, como información complementaria.

– Después de haber trabajado el doble podemos aprovecharlo a través de su reversibilidad: 10 es el doble de 5 y 5 es la mitad de 10. La mitad de 10 es 5 porque 10 = 5 + 5

– También se hará con números impares para que se den cuenta que esas cantidades no se pueden repartir por el momento en 2 grupos iguales.

– Una vez hemos trabajado con unidades haremos el mismo trabajo con decenas completas, es decir, cogerán una cantidad de material que forme el número 40 que son 4 D y luego tendrán que repartirla en 2 grupos que contengan la misma cantidad, en este caso de 20. Es muy importante trabajar la mitad específicamente de decenas completas como son el 30, 50, 70 o 90 ya que se darán cuenta que al dividir esas cantidades en 2 grupos iguales, tendrán que deshacer una decena en unidades para poder hacerlo.

– Por último se hará lo mismo con las centenas. Al igual que pasaba con las decenas cuando hagamos la mitad del 300, 500, 700 y 900 se tendrá que deshacer una centena en 10 decenas para continuar con el reparto.

– De esta manera se quiere conseguir que cuando quiera calcular la mitad de un número de 3 cifras como pueda ser el 472, lo haga primero calculando el mitad de cada una de las unidades. De esta manera calculará el mitad de 400, el de 70 y el de 2 por separado para luego juntar todas las cantidades: 200 + 35 + 1 = 236

– Para trabajar la primera parte de los polígonos sería conveniente llevarse objetos o bien que tengamos en clase o traerlos de casa para mostrarlos y que vayan diciendo cuáles son polígonos y cuáles no.

– Para seguir con la misma tarea serán ellos los que nos digan objetos que  tienen polígonos y objetos que no.

– En esta página estamos sumando números de 3 cifras formado por decenas completas como por ejemplo 270 con decenas completas como 80.

– A la hora de resolver este tipo de operaciones es mucho más sencillo de hacerlo si ponemos en práctica algo que llevamos bastante tiempo realizando como sería el tener claro que el 270 está formado por 27 D y el 80 por 8 D, de manera que habría que sumar 27 + 8 = 35 D o lo que es lo mismo 350 unidades. 

– Podemos empezar por tener 20 objetos pequeños diferentes como tijeras, lápiz, goma, grapadora, rotulador…y colocarlos en orden encima de una mesa. Posteriormente se les irá preguntando:

En qué posición se encuentra la grapadora???

Qué objeto se encuentra antes del decimoquinto???

Qué objeto hay entre el octavo y el décimo???

Cuál es la posición posterior al rotulador??

– También, para que una actividad de ordenación sea más significativa para los niños, se pueden realizar actividades vivenciales en las que ellos mismos son los “objetos” a ordenar. Se pueden ordenar los nombres de los peques de la clase o ir al patio y hacer una fila con todos los peques y que cada uno identifique delante y detrás de quién están o que se coloquen en un orden según una indicación que le hayamos dado por escrito.

– Comenzaremos midiendo con regla objetos pequeños para trabajar el cm.

– Después diremos de medir objetos más grandes para que se den cuenta que con la regla sería muy difícil medirlo pues necesitaríamos varias. Es el momento de introducir el metro. Mediremos varios elementos con el metro para luego plantearle medir distancias más grandes. Ahora se darán cuenta que necesitaríamos varios metros y es el momento de explicarles el km.

– Posteriormente les pediremos que sean ellos los que vayan diciendo objetos o situaciones que se puedes medir con las diferentes unidades de medidas explicadas.