Libro de Primero - Los Mateamigos y la Máquina del Tiempo
- Unidad 1 – ¿POR QUÉ HAY TANTOS DINOSAURIOS EN EL BOSQUE?
- Unidad 2 – ¿QUIÉN HA PINTADO BISONTES EN ESTA CUEVA?
- Unidad 3 – ¿QUIÉN HA CONSTRUIDO ESTAS PIRÁMIDES TAN GRANDES?
- Unidad 4 – ¿QUIÉN ES ESE SEÑOR CON ARMADURA?
- Unidad 5 – ¿QUIÉN HA DESCUBIERTO AMÉRICA?
- Unidad 6 – ¿POR QUÉ HAY TANTO HUMO EN ESTA CIUDAD?
- Unidad 7 – ¿POR QUÉ VUELAN LOS COCHES?
- Unidad 8 – ¿CUÁNTO TIEMPO HEMOS VIAJADO POR EL TIEMPO?
Exámenes
Libro de Quinto - Los Mateamigos y la Máquina Misteriosa
Cuaderno de Sexto - Los Mateamigos y la Puerta Interdimensional
Libro de Segundo - Los Mateamigos y el Libro Mágico
Índice Didáctico
Unidad 1 – ¡UNA NIÑA CON CAPERUZA ROJA!
Juego relacionado con los contenidos que se van a trabajar.
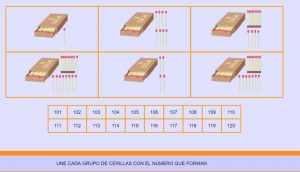
– Para empezar podemos seguir utilizando el mismo material manipulativo que en primero. En este caso valdría palillos, piedrecitas, tapones, material multibase etc, pero lo que tenemos que tener claro es que se tiene que poder formar decenas y centenas.
– Para formar las centenas desde el inicio pedimos a los niños que formen decenas para que luego unan 10 para componer la centena. Este paso es importante al igual que el de descomponer la centena en 10 decenas para la comprensión de los números de 3 cifras.
– Cómo actividades previas podemos ir pidiendo que vayan formando números que vamos diciendo partiendo desde cero, es decir, todos los palitos o material a utilizar suelto.
– Si tenemos pizarras borrables podemos utilizar simbología de manera que puedan dibujar los símbolos necesarios para formar un número o adivinar un número partiendo de una composición dada. Los símbolos realmente pueden ser los que se estimen oportunos, nosotros por ejemplo utilizamos palito para la unidad, círculo decena y triángulo la centena. Para los que utilicen material multibase puede valer cuadradito, rectángulo y cuadrado grande.
– Al igual que hemos trabajado los complementarios del 10 y del 100 buscamos ahora completar números hasta el 200.
– Se puede hacer de diferentes maneras ya que habrá quien lo haga de manera ascendente incorporando lo que falta hasta llegar al 200.
En este caso, previamente, podemos formar el número del que partimos tanto con objetos manipulativos que utilizamos como con simbología y simplemente vamos añadiendo las unidades y decenas que nos faltan para completar. Finalmente tendremos que juntar todo lo que hemos ido añadiendo hasta llegar al 200.
– Para aquellos que no lo quieren hacer de manera ascendente pueden directamente partir del 200. En este caso formamos con material o simbología el 200 para seguidamente ir quitando las cantidades de las que partíamos. Es necesario dominar la descomposición ya que si al 200 hay que quitarle por ejemplo 70 el alumno tiene que saber que una centena del 200 se tienen que convertir en 10 decenas para poder quitarle 7 y así sucesivamente si también queremos utilizar las unidades.
Vídeo relacionado con los contenidos que se van a trabajar.
Presentación relacionada con los contenidos que se van a trabajar.
Juego relacionado con los contenidos que se van a trabajar.
– Llega el momento en el que hay que empezar a descomponer números de 3 cifras. Para empezar es básico que antes se hayan hecho los ejercicios manipulativos que hemos ido diciendo. Es fundamental que el alumno manipule de manera que convierta una centena en decenas, una centena en unidades y viceversa. Del dominio y compresión de esto dependerá su fluidez para la realización de las descomposiciones.
– Para ello podemos pedir a los alumnos primero que formen un número, todos el mismo y en la pizarra se van a ir diciendo descomposiciones posibles que se puedan dar. Al inicio podemos orientarlos nosotros. Es normal que mantengan la centena en la columna de las centenas y no la pongan en las decenas ya que este es el nuevo concepto que tiene que aprender y por lo tanto solo descompongan decenas y unidad como hacían en el curso anterior.
– Cómo recurso para la comprensión se puede utilizar el color de cada una de las distintas unidades de manera que le podemos decir a los niños que al terminar una descomposición tenemos que darnos cuenta de que el número de centenas que hemos puesto coincide con el del número a descomponer al igual que las decenas y unidades.
– De igual forma cuando tenemos una descomposición incompleta podemos ir mirando cada unidad por separado y ver de qué unidad nos falta algo. Es importante que también piensen en cada una de las unidades por separado.
Vídeo relacionado con los contenidos que se van a trabajar.
Presentación relacionada con los contenidos que se van a trabajar.
Juego relacionado con los contenidos que se van a trabajar.
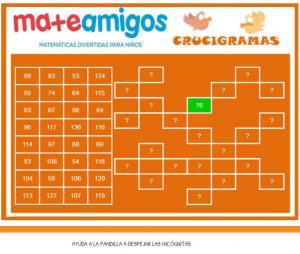
– Nos encontramos con crucigramas que ya hemos resuelto en el curso anterior. Para recordarlo partimos de que cuando vamos a la casilla anterior estamos restando una unidad, si vamos a la posterior la sumamos, si subimos estamos restando una decena y si bajamos la restamos.
– La dificultad de la tarea ahora radica en que el alumno encontrará dificultades cuando se encuentre con una frontera. Nos referimos a frontera cuando al 92 por ejemplo le vamos a sumar una decena y llega al 102. Ese paso y cambio de centena lo podemos llamar frontera.
Para la comprensión de este ejercicio es básico dominar algo que ya hemos comentado anteriormente y es el dominio de cada una de las unidades. Tenemos que tener claro que sumar 10 es sumar 1 D por lo que si al 92 hay que sumarle una decena igual para el alumno es mucho más fácil decir 9 D + 1 D son 10 D que con las 2 U forman el 102 que decirles 92 + 10 que seguramente tendrán que contar de 1 en 1 y lo ven más complicado.
Al igual que su decimos 105 – 10 lo ven más difícil que si decimos 10 D – 1 D igual a 9 D que junto con las 5 U forman el 95.
– El control de este tipo de ejercicios es fundamental para realizar más fácil multitud de tareas que a lo largo de los cursos se irán encontrando.
– Para este tipo de ejercicios al inicio también podemos utilizar la tabla de la frontera del 100 que es como una tabla del 100 pero con los números hasta el 150.
Vídeo sobre los contenidos que se van a trabajar.
Presentación sobre los contenidos que se van a trabajar.
– Tras explicar con ejemplos cuando un número es par o impar siempre podemos comenzar a trabajarlo con el típico juego de «pares o nones». Por parejas uno elige pares y otro nones y a la de tres sacan los dedos que quieran de las dos manos. Una vez lo hagan se cuenta los dedos y gana aquel que haya elegido lo que ha salido. Se compite al mejor de tres y el que ha perdido cae eliminado y los que han ganado pasan a la siguiente ronda hasta que solo quede uno.
– También podemos seguir series numéricas de números pares o impares partiendo de un número que digamos y que vayan diciendo rápidamente cuál sería el siguiente.
Juego relacionado con los contenidos que se van a trabajar.
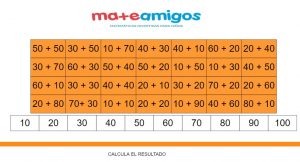
– En esta página resolvemos pirámides numéricas con decenas completas. Para ello seguimos poniendo en práctica lo mismo que hemos trabajado en las actividades anteriores relacionados con la importancia de trabajar la cantidad de cada una de las unidades.
Para ello podemos ir poniendo diferentes sumas con decenas completas como por ejemplo 70 + 80. En este caso y con lo que hemos estado diciendo seguro que es más fácil para el alumnos sumas 7 D + 8 D que son 15 D o lo que es lo mismo 150 unidades, que coger todas las unidades y sumarlas con la dificultad de que hay una frontera por medio. Del manejo de esta habilidad dependerá en gran medida la rapidez en cálculo mental de nuestros alumnos.
– Seguidamente podemos poner ejemplos con números de 3 cifras como puede ser 280 + 250. Si pensamos en decenas completas sumaríamos 28 D + 25 D que son 53 D o lo que es lo mismo 530 U.
– Antes de comenzar a resolver la actividad también podemos hacer lo mismo pero en el caso de la resta.
– En esta página trabajamos directamente la estimación de longitud, peso y medida. Para ello podemos utilizar actividades parecidas a las de primero para recordar.
– Podemos utilizar diferentes recipientes. Sobre todo con los que usan habitualmente: tetrabriks, vasos, latas de refresco, botellas y bidones de agua, envases de yogurt. Con ellos se pueden hacer multitud de actividades como ordenarlos de mayor a menor o viceversa según su capacidad, llenarlos para saber cuántos se necesitan de un más pequeño para llenar uno más grande, partiendo de uno que tenga un litro vaciarlo en lo demás para saber si tiene más o menos de 1 litro…
-Se enseña a los niños diferentes objetos que procederán a clasificarlos muy pesados, en peso medio y poco pesados utilizando sus manos para percibirlo.
– Para trabajar la medida podemos darle un objeto de referencia con una medida concreta para que nos vayan diciendo en primer lugar objetos que midas más para terminar diciendo otros que midan menos.
Vídeo relacionado con los contenidos que se van a trabajar.
Presentación sobre el contenido que se va a trabajar.
– Tras presentar como se mide con el palmo, pie y paso procedemos primero a que midan diferentes objetos o estancias con cada uno de ellos. Por ejemplo podemos medir el ancho o largo del libro, de la mesa, de la clase o incluso si salimos al patio podemos medir el ancho o largo de la pista, la portería, el banco… Una vez medido y si han anotado las mediciones se pueden comparar las de unos con otros para que se den cuenta de que no han obtenido los mismos resultados para después preguntarles ¿qué creéis que ha sucedido?
– Otro tipo de actividad que se puede hacer sin necesidad de medir pero si para que reflexionen sobre que unidad (mano, pie o paso) es más recomendable utilizar, sería ir diciendo objetos y que vayan diciendo la unidad que utilizarían para medirlos.
Juego relacionado con los contenidos que se van a trabajar.
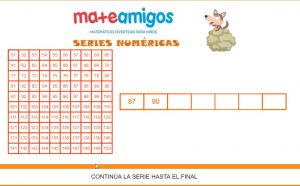
– Encontramos dos tipos de series numéricas. Unas en las que sumamos o restamos unidades sueltas y otras en las que lo hacemos con decenas completas.
– Podemos resolver series conjuntas para indicarles los pasos que pueden seguir para no equivocarse. Estos pasos podrías ser 3:
1.° Ver si la serie es ascendente o descendente poniendo el símbolo + en caso de ser ascendente o – si es descendente.
2.° Averiguar la cantidad que va desde un número a otro de los que nos dan. Para ello hay únicamente que contar partiendo del número siguiente del que estamos en caso de la suma o del anterior en caso de resta.
3.° Por último hay que resolverla pues ya sabemos la cantidad que hay que sumar o restar para llegar al próximo número.
– Si estamos sumando y restando unidades únicamente tendrán que ir sumando o restando la cantidad partiendo del número completo, es decir, si la serie es 75-69-X, partimos del 69 y vamos contando hacia atrás 6 para llegar al 63.
– En el caso de que sean decenas completas podemos pensar en decenas y resultará más fácil. Por ejemplo si las serie es 184-164-X y el 164 tiene 16 D le quitamos 2 D para que se quede en 144.
En esta página comenzamos a trabajar problemas sencillos de sumar y restar, de las categorías semánticas CAMBIO y COMBINACIÓN.
Problema 1.Categoría: CAMBIO 1
Justificación: La cantidad inicial (castañas que tenía la abuela) se transforma a través de un aumento (castañas que ha recogido Caperucita para su abuela) y se convierte en la cantidad final (desconocida). Operación: 56 + 29 = 85.
Problema 2.Categoría: CAMBIO 2
Justificación: La cantidad inicial (árboles del año pasado) se transforma a través de una disminución (árboles talados) y se convierte en la cantidad final (desconocida).Operación: 161 – 35 = 126.
Problema 3.Categoría: CAMBIO 2
Justificación: La cantidad inicial (páginas del libro) se transforma a través de una disminución (páginas leídas) y se convierte en la cantidad final (desconocida).Operación: 155 – 88 = 67.
Problema 4.Categoría: COMBINACIÓN 1
Justificación: Los elementos de dos conjuntos (las setas recogidas por la mañana y por la tarde) se combinan para formar un todo (desconocido).Operación: 65 + 104 = 169
– Para empezar comenzamos repasando de nuevo los números pares con alguna de las actividades propuestas anteriormente.
– Seguidamente tendremos que resolver dos tipos de operaciones. Por un lado sumas y restas de números de 3 cifras a las que les sumamos o restamos unidades y por otro lado operaciones en las que sumamos o restamos decenas completas.
– La intención es que este tipo de cálculo lo hagan mentalmente siguiendo las mismas estrategias que en las series numéricas anteriores:
– Si estamos sumando o restando unidades únicamente tendrán que ir sumando o restando la cantidad partiendo del número completo, es decir, si sumamos 247 + 8 partimos del número mayor y contamos hacia adelante en este caso las unidades que tenemos
– En el caso de que sean decenas completas podemos pensar en decenas y resultará más fácil. Por ejemplo si la resta es 231 – 90 partimos de que el 231 tiene 23 D – 9 D nos da como resultado 14 D que junto a las unidades que teníamos obtenemos el resultado de 141.
Para resolver las sumas os dejamos algunas presentaciones de distintas formas de hacerlas.
SUMAMOS DE MANERA POSICIONAL
SUMAMOS POR DESCOMPOSICIÓN
SUMAMOS DE MANERA ABIERTA
Vídeos sobre algunas maneras de resolver las sumas.
SUMAMOS DE MANERA POSICIONAL
SUMAMOS POR DESCOMPOSICIÓN
SUMAMOS DE MANERA ABIERTA
Para resolver las restas os dejamos algunas presentaciones de distintas formas de hacerlas.
RESTAMOS DE MANERA POSICIONAL
RESTAMOS POR DESCOMPOSICIÓN
RESTAMOS DE MANERA ABIERTA
Vídeos sobre algunas maneras de resolver las restas.
RESTAMOS DE MANERA POSICIONAL
RESTAMOS POR DESCOMPOSICIÓN
RESTAMOS DE MANERA ABIERTA
– En esta página resolvemos las primeras sumas y restas con números de 3 cifras. En el apartado de materiales de la intranet podréis encontrar 3 de las muchas formas en la que se pueden resolver estos algoritmos.
– Dejamos que cada docente elija el algoritmo que mejor se ajuste al alumnado que tenga siempre y cuando se trabaje sea explicado con sentido y no para resolverlo de manera mecánica.
– En nuestra clase hay alumnos que lo resuelven de una manera y otros de otra.
Vídeo relacionado con los contenidos que se van a trabajar.
Presentación relacionada con los contenidos que se van a trabajar.
– Se puede repartir lana, una cuerda, plastilina etc… y tras explicar que tipos de líneas podemos encontrar que vayan representando la que se vaya diciendo.
-Se puede dibujar un tipo de línea en la pizarra y que los alumnos tengan que adivinar de qué tipo es.
-El docente escribe el nombre de un tipo de línea y el alumno tiene que representarla en su pizarra o folio.
-Ir analizando objetos que nos rodean para ver qué tipo de líneas tienen o decir un tipo de línea y que los alumnos tengan que buscar que objetos las tienen.
– Dibujar en la pizarra borrable objetos con líneas y que luego adivinen que objeto es y qué líneas si han utilizado.
En esta página trabajamos problemas de sumar y restar de la categoría semántica COMBINACIÓN.
Problema 1. Categoría: COMBINACIÓN 1
Justificación: Los elementos de dos conjuntos (las fotos de un álbum y las del otro) se combinan para formar un todo (desconocido).Operación: 84 + 107 = 191.
Problema 2. Categoría: COMBINACIÓN 2
Justificación: Los elementos de dos conjuntos (los patos que están dentro del lago y los que están fuera de él) se combinan para formar un todo (el total de patos). Conocemos el total y los patos que están dentro y nos preguntan por los que están fuera. Desconocemos una parte del todo. Operación: 91 – 57 = 34.
Problema 3. Categoría: COMBINACIÓN 2
Justificación: Los elementos de dos conjuntos (los bombones de chocolate blanco y los de chocolate negro) se combinan para formar un todo (el total de bombones). Conocemos el total de bombones y la cantidad de bombones de chocolate negro y nos preguntan por los de chocolate blanco. Desconocemos una parte del todo. Operación: 100 – 63 = 37.
Problema 4. Categoría: COMBINACIÓN 1
Justificación: Los elementos de dos conjuntos (las hormigas rojas y las negras) se combinan para formar un todo (desconocido).Operación: 49 + 96 = 45.
– Para comenzar podemos pedir a los alumnos que nos digan cuántos focos de luz, por ejemplo, hay en la clase para seguidamente continuar preguntando por otros objetos.
– Podemos seguir preguntando por características o partes de nuestro cuerpo como cuántos niños y niñas rubios hay en la clase o cuántas manos hay en total. También podemos utilizar la vestimenta.
– Aunque estas actividades de conteo pensemos que están más bien orientadas a cursos inferiores en realidad ayudan a trabajar la atención y la agudeza visual entre otras cosas.
– Por último con los datos anotado podemos continuar preguntado por ejemplo, ¿cuántos más pájaros que ardillas hay?, ¿cuántos animales aparecen en la imagen?…
Repaso
Los Mateamigos
Copyright © José Ángel Tudela Corbalán
Autores: Fran Franco Galvín / José Ángel Tudela Corbalán
Escritor: Pedro Pujante Hernández
Ilustración y maquetación: Bibe Sánchez
Diseño Web: José María Cánovas Martínez
Editado por José Ángel Tudela Corbalán.
Reservados todos los derechos. No se permite la reproducción total o parcial de nuestros libros, ni su incorporación a un sistema informático, ni su transmisión en cualquier forma o por cualquier medio (electrónico, mecánico, fotocopia, grabación u otro) sin la autorización previa y por escrito de los titulares del copyright. La infracción de dichos derechos puede constituir un delito contra la propiedad intelectual.
0 comentarios